AVL Tree, B-Tree, dan Red-Black Tree

AVL TREE

• AVL Tree merupakan bentuk binary tree yang diseimbangkan, di mana perbedaan antara ketinggian sub pohon kiri dan kanan tidak boleh lebih dari satu untuk semua node.
• Tujuan AVL Tree adalah mempersingkat dan menyederhanakan waktu pencarian dari suatu data.

Contoh AVL Tree
Sumber : https://www.geeksforgeeks.org/avl-tree-set-1-insertion/

Contoh binary tree biasa (bukan AVL Tree)
Sumber : https://www.geeksforgeeks.org/avl-tree-set-1-insertion/

• Operasi dalam AVL Tree meliputi :

1. Insert
• Left-Left Case (Single Rotation)
• Right-Right Case (Single Rotation)
• Left-Right Case (Double Rotation)
• Right-Left Case (Double Rotation)
2. Delete
• Jika node yang akan dihapus berada pada posisi leaf atau node tanpa anak, maka dapat langsung di hapus.

• Jika node yang akan dihapus memiliki anak, maka proses penghapusannya harus di cek kembali untuk menyeimbangkan Binary Search Tree dengan perbedaan tinggi / level maksimal 1.

• Single Rotation dan Double Rotation
• Single rotation dilakukan bila kondisi AVL tree waktu akan ditambahkan node baru dan posisi node baru seperti pada gambar 2. T1, T2, dan T3 adalah subtree yang urutannya harus seperti demikian serta height- nya harus sama (≥ 0). Hal ini juga berlaku untuk AVL tree yang merupakan citra cermin (mirror image).

Sumber : http://dinda-dinho.blogspot.com/2013/06/pengertian-dan-konsep-avl-tree.html

• Double rotation dilakukan bila kondisi AVL tree waktu akan ditambahkan node baru dan posisi node baru seperti pada gambar 3. T1, T2, T3, dan T4 adalah subtree yang urutannya harus seperti demikian. Tinggi subtree T1 harus sama dengan T4 (≥ 0), tinggi subtree T2 harus sama dengan T3 (≥ 0). Node yang ditambahkan akan menjadi child dari subtree T2 atau T3. Hal ini juga berlaku untuk AVL tree yang merupakan citra cermin (mirror image).

Sumber : http://dinda-dinho.blogspot.com/2013/06/pengertian-dan-konsep-avl-tree.html

• CONTOH :
• * insert: 5,6,7,0,4,3,8
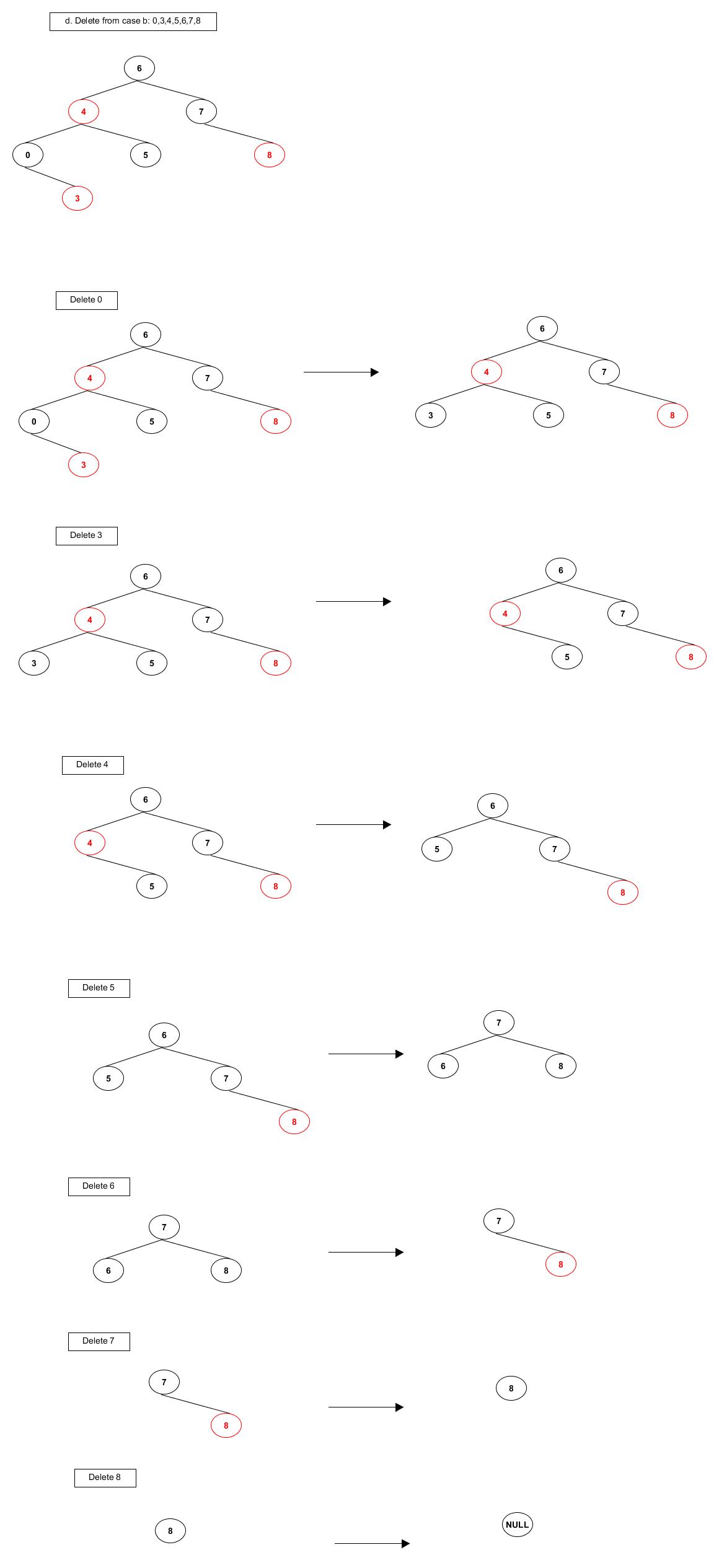
• * delete: 3,4,8

B-TREE

• B-Tree adalah bagian dari binary tree, dimana bentuk penyederhanaan dan penyeimbangan sekaligus dari binary tree.
• Aturan pada B-Tree : m = order
• Setiap node (kecuali leaf) memiliki anak paling banyak sejumlah m anak
• Setiap node (kecuali root) memiliki anak paling sedikit m/2 anak
• Root memiliki anak minimal 2, selama root bukan leaf
• Jika node non leaf memiliki k anak, maka jumlah data yang tersimpan dalam node k-1
• Data yang tersimpan pada node harus terurut secara inorder
• Semua leaf berada pada level yang sama, level terbawah

Sumber : http://suciantinovi.blogspot.com/2014/05/b-tree-and-heap-deap.html

• Operasi pada B-Tree
• Insert

• Anggap data yang mau di insert adalah key
• Posisikan key pada node yang sesuai, seperti pada BST dan 2-3 Tree, anggap node tersebut A
• Jika A adalah node dengan jumlah data kurang dari m-1, maka langsung masukan saja
• Jika A adalah node dengan jumlah data m-1, maka masukan nilai tengah kemudian masukan ke parentnya. Kemudian anggaplah parent tersebut A. Kemudian periksa kembali sesuai aturan point ke 3 dan 4.

• Search
• Searching pada B-Tree mirip seperti 2-3 Tree. Pertama-tama kita bandingkan dengan rootnya terlebih dahulu kemudian cek apakah sama dengan rootnya atau lebih kecil atau lebih besar atau bahkan diantara rootnya (jika root memiliki lebih dari 1 data).

• Delete
• Anggap node yang mau di delete adalah key
• Delete dilakukan pada leaf. Meskipun pada saat menghapus node parent, kita tetap menganggapnya menghapus leaf, karena ketika parent dihapus lalu digantikan oleh anak terbesar subtree kiri atau anak terkecil subtree kanan sama saja kita seolah-olah menghapus anak yang menggantikannya. dimana anak tersebut selalu berada pada posisi leaf. maka leaf tersebut dianggap P.
• Jika ukuran P > m/2 maka langsung delete saja data yang ingin dihapus
• Jika ukuran P = m/2 maka : perhatikan siblingnya (anggap sibling adalah Q)
• Q > m/2, maka rotasi pada P
• Q = m/2, satukan P dan Q

RED-BLACK TREE

Contoh kasus:

a. Insert 1,2,3,4,5,6,7,8.

b. Insert 5,6,7,0,4,3,8

c. Delete from case a: all prime number in sequence, (hapus deret prima dari paling kecil)

d. Delete from case b: 0,3,4,5,6,7,8